o mně / blog / poezie / obrazy / životopis / weby / senát / kontakt
Kaleidoskop 2019/1
Rozumíte riziku? Dokážete správně vyhodnotit možný zisk a ztrátu?

Riziko zisku a ztráty hodnotíme denně neustále (intuitivně), aniž bychom si to vůbec uvědomovali.
Například:
- Mám si dát oběd v této nové a neznámé restauraci? Vypadá luxusně, ale bude i dovednost kuchaře stejně přepychová?
- Mám podat odvolání proti pokutě, kterou jsem obdržel od policie? Jakou mám šanci, že uspěji nebo jaká je pravděpodobnost, že mi naopak ještě zpřísní trest?
- Mám vzít jistou výhru nebo se pustit do dalšího kola loterie s tím, že možná nevyhraji vůbec nic?
- Je rozumné jít na operaci, když je šance na úspěch 95%?
- atp.
O malých rizicích rozhodujeme doslova na každém kroku a to především intuitivně. Nemáme totiž obvykle dost času ani informací, abychom prováděli složité rozbory situací. Co víc, například i akciové trhy jsou založeny na předpokladu, že člověk jedná v každé chvíli racionálně, resp. dokáže správně vyhodnocovat rizika a maximalizovat svůj užitek (zisk).
Zkuste si prosím udělat nejprve malý test, který Vám posléze ukáže, jak riziko hodnotíte Vy sami. Jedná se o tři po sobě jdoucí otázky (experimenty), v nichž si máte zvolit buď řešení A nebo B, podle toho, které se Vám zdá lepší. Volíte vždy mezi možností výhry a prohry, která je doprovázena jinou mírou rizika.
Test
První otázka nabízí poměrně jednoduché rozhodnutí: "Chcete A) obdržet 1000 Kč bez jakéhokoli rizika prohry, nebo se rozhodnete pro možnost B), kde je lákavý vyšší zisk 5000 Kč, avšak za cenu, že můžete odejít i s 0 Kč?"
Záleží tedy na Vás, zda preferujete jistotu či ne. Přesněji řečeno, zda se Vám riziko zdá přiměřené, nebo dokonce lepší, než daná jistota.
Poznamenejte si prosím Vaše odpovědi třeba tužkou na papír. Poté se podíváme na vyhodnocení.



Vyhodnocení
A nyní se zaměřme na vyhodnocení. Jednotlivé možnosti jsem graficky znázornil a porovnal mezi sebou tak, aby rozdíly byly zřetelné.
Na vodorovné ose X se nachází škála 0 až 100% a ní jsou do výšky podle možné výhry (prohry) vztyčeny sloupečky (osa Y).
Experiment 1
Možnost 1A nabízí ve sto procentech 1000 Kč, takže se jedná jen o jednoduchou rovnou čáru.

Možnost 1B pro změnu ukazuje tři varianty. Nejvíce místa zabírá čtverec 89% s výhrou 1000 Kč, 10% s výhrou 5000 Kč je znázorněn jako šipka, protože se celý nevejde do stupnice (osa Y končí 1000 Kč) a konečně malý přerušený úsek představuje nulovou výhru 1%.

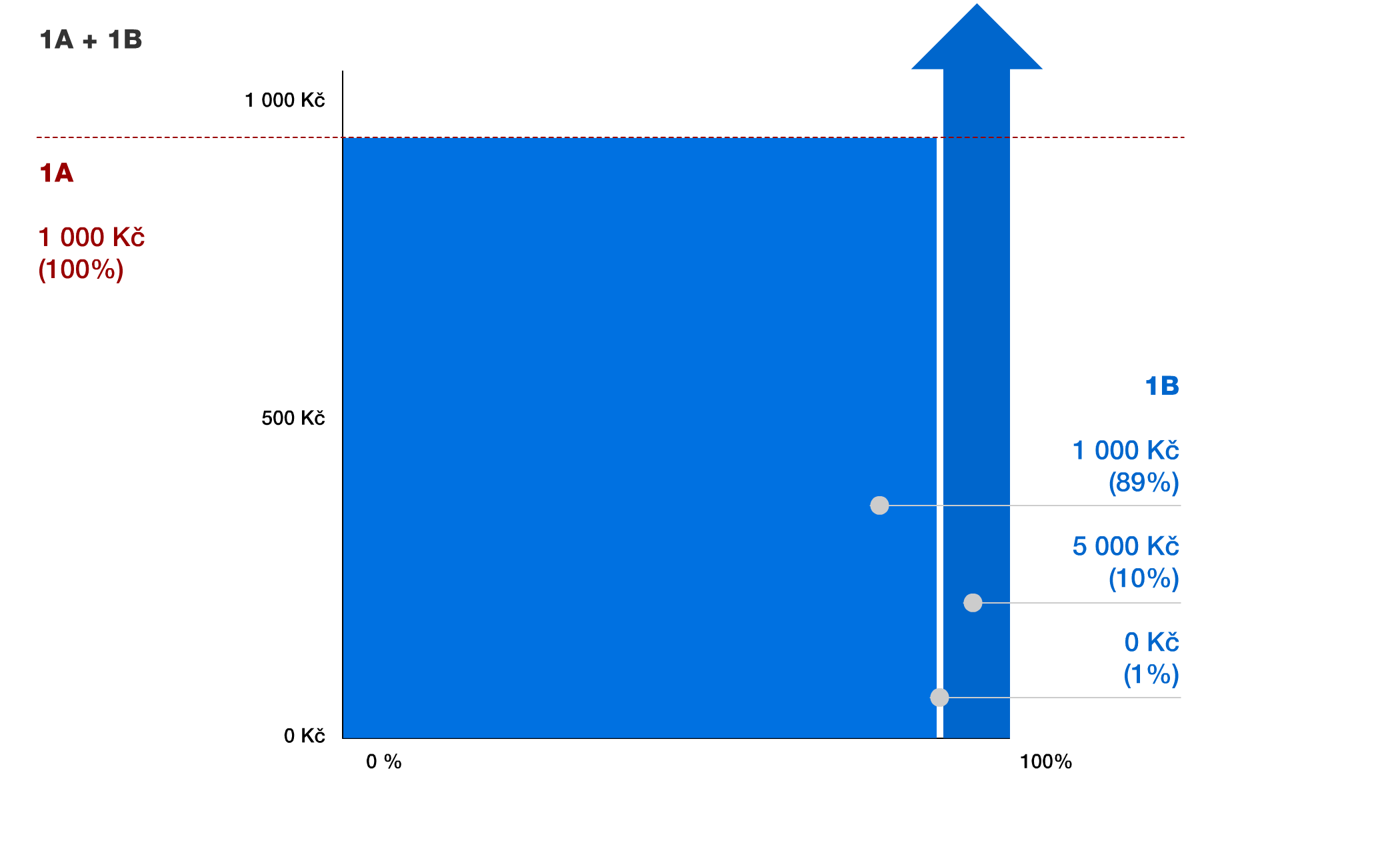
1A + 1B: Nyní je potřeba oba grafy položit přes sebe, aby bylo vidět, jak se výhra či prohra od sebe liší.
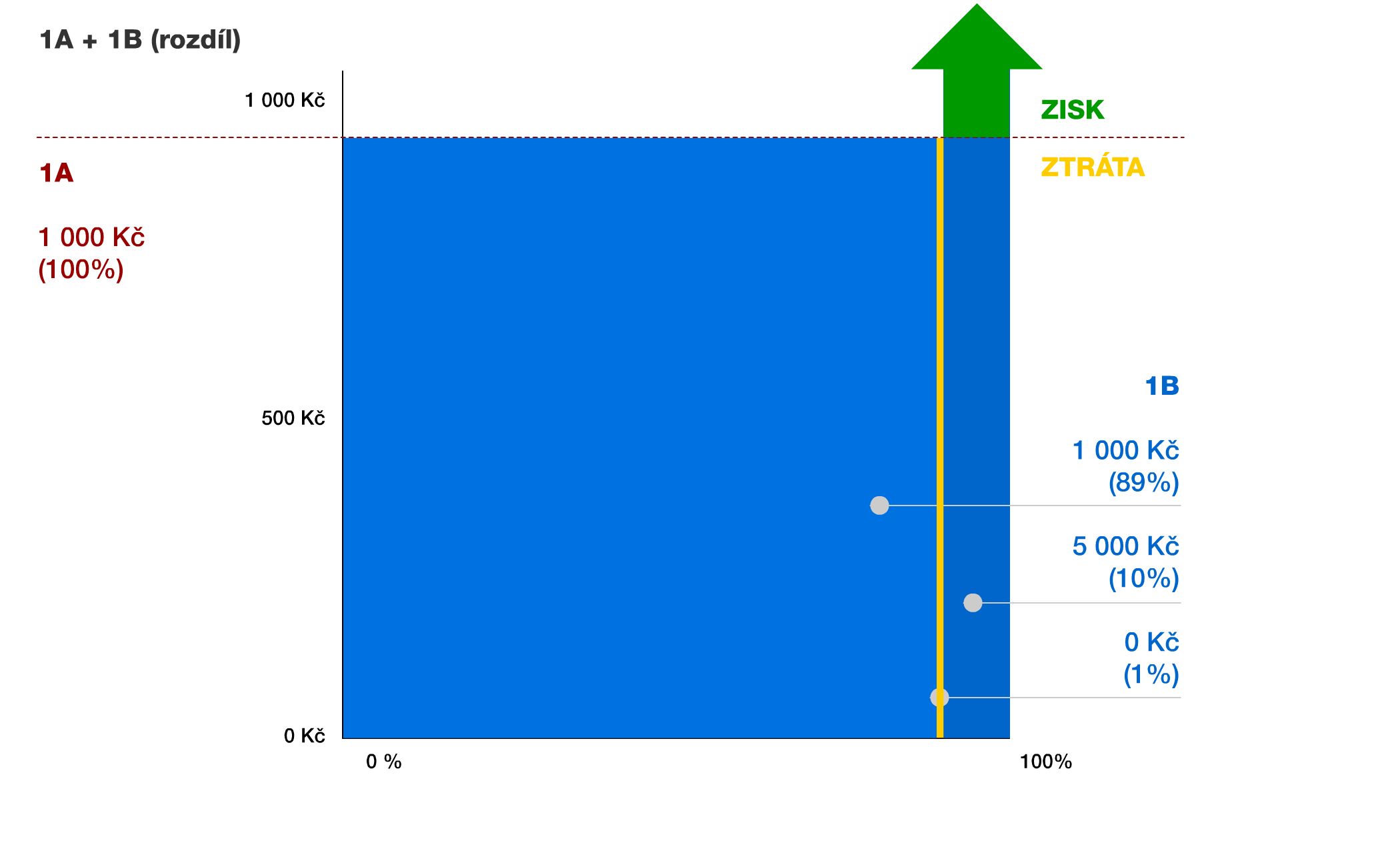
1A + 1B (rozdíl): Aby bylo porovnání zřejmější, vyznačil jsem pro možnost 1B zisk (zeleně) a ztrátu (žlutě), kterou se 1B liší od možnosti 1A. Jak je patrné, možný zisk při volbě 1B je mnohem vyšší (šipka pokračuje až do výše 5000 Kč), než hrozící neúspěch v podobě titěrného žlutého sloupečku 1% s nulovou výhrou. Racionální volbou je tedy 1B, protože možný zisk výrazně převyšuje možnou ztrátu v porovnání s 1A. Pokud jste ale vybrali možnost 1A, nebuďte smutní. Stali jste se patrně obětí vlastní intuice, která má tendenci dávat nepatřičně vysokou váhu nízkým pravděpodobnostem (tabulka na závěr článku).
Experiment 2
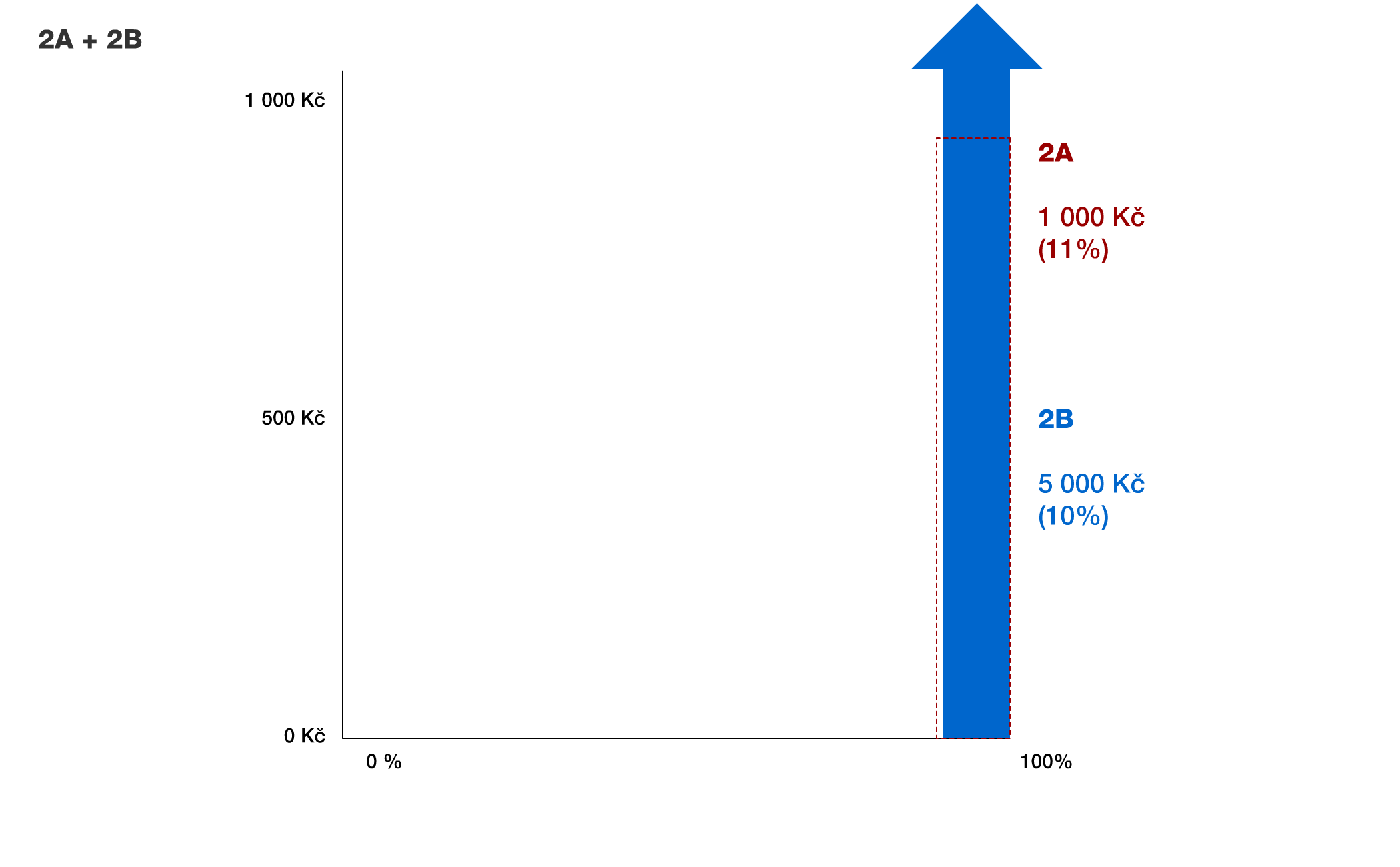
Možnost 2A je jednoduchá. Jedná se o sloupeček s šířkou 11% ve výši 1000 Kč. Zbytek pole neposkytuje žádnou možnost výhry.

2A + 2B: ukazuje porovnání, jak se od sebe liší obě možnosti. 2B je jen nepatrně užší, ale mnohem vyšší (šipka pokračuje až do výše 5000 Kč).
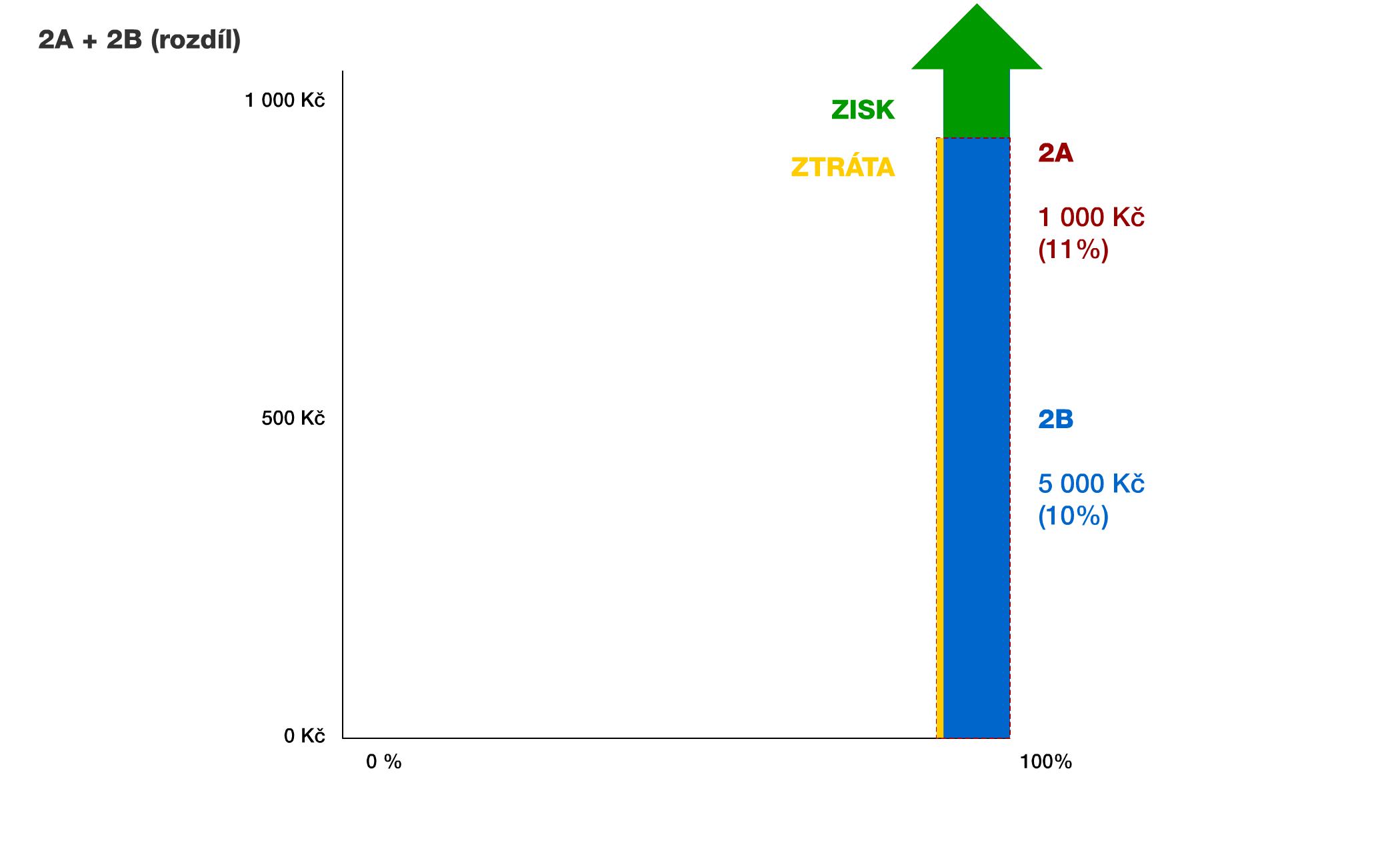
2A + 2B (rozdíl): kdo volil variantu 2A bude patrně zklamán při pohledu na porovnání zisku (zeleně) a ztráty (žlutě), protože 2B je opět racionální volbou pro všechny, kteří jsou ochotni podstoupit nepatrně vyšší riziko (+1% možný neúspěch) proti pětinásobnému zvýšení zisku. Co je však ještě překvapivější – ten kdo zvolil v případě experimentu 1 a experimentu 2 jinou možnost (tedy 1A+2B nebo 1B+2A), měl by se chytit za hlavu, protože jednal naprosto rozporuplně. Pokud si totiž obrázek "2A + 2B (rozdíl)" porovnáte s výše uvedeným "1A + 1B (rozdíl)", zjistíte, že zelená a žlutá oblast jsou vlastně úplně shodné. Položíte si tedy otázku, proč se Vám v jednom případě 1% s nulou zdálo tak významné a ve druhém nikoliv? Odpověď je naprosto stejná, ale pro jistou ji zopakuji: Stali jste se patrně obětí vlastní intuice, která má tendenci dávat nepatřičně vysokou váhu nízkým pravděpodobnostem (tabulka na závěr článku).
Experiment 3
U třetího příkladu je potřeba dávat pozor na to, že řešíme jistou ztrátu v porovnání se ztrátou nejistou. Vyšší sloupce tedy znamenají horší výsledek.
Možnost 3A je jednoduchá. Jedná se o konstantní ztrátu -100 Kč.
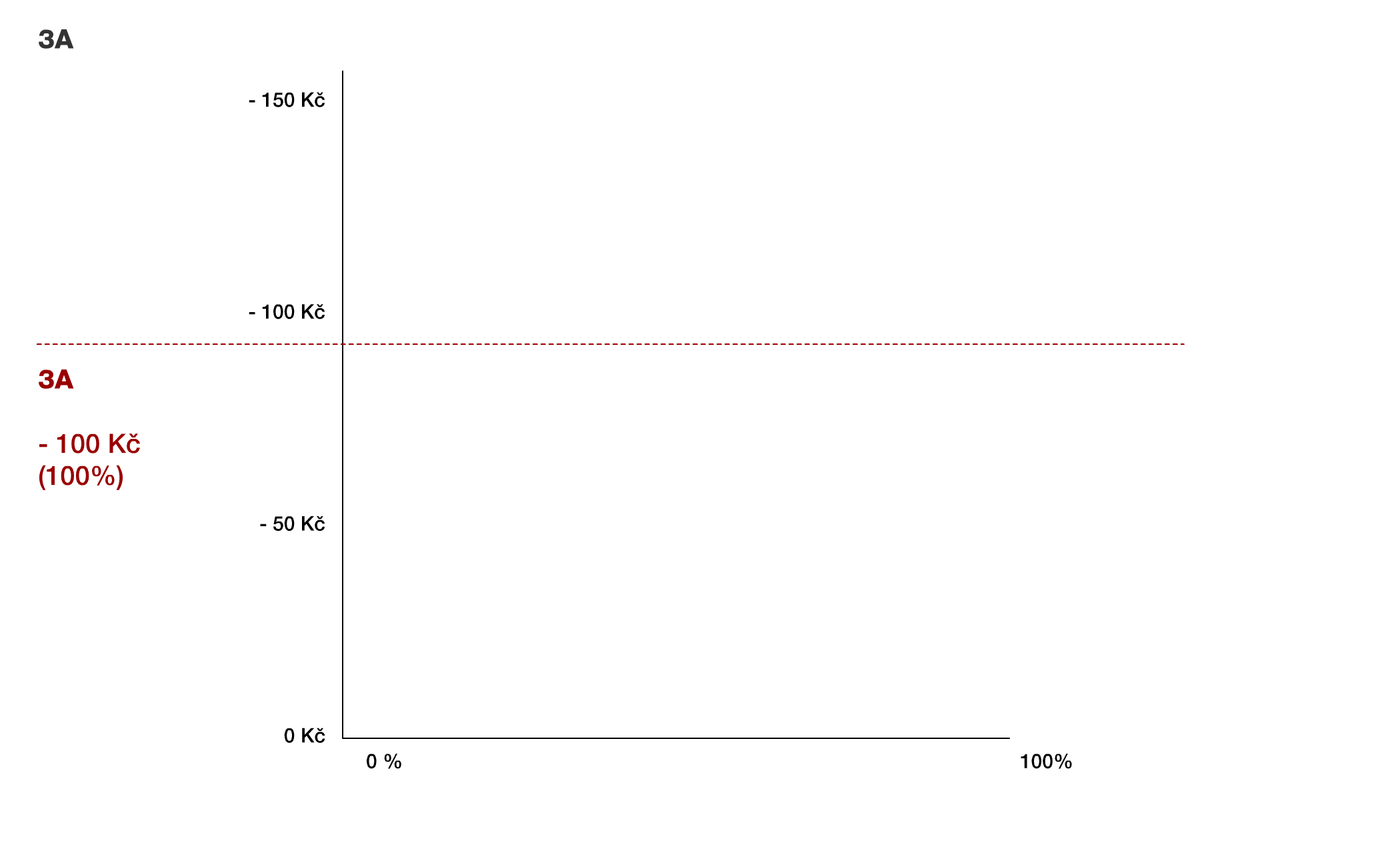
3A + 3B ukazuje porovnání, jak se od sebe liší obě možnosti.

3A + 3B (rozdíl): jak je již od pohledu patrné, volba 3B s sebou nese nesrovnatelně vyšší riziko ztráty (žlutá) proti konstantní variantě 3A. Přesto je varianta 3B velmi oblíbenou odpovědí. Myslíte, že je to překvapivé? Vůbec ne.

Závěr
Podle dlouhodobých výzkumů se totiž ukazuje, že většina lidí je v oblasti možného zisku zbytečně konzervativní a neriskuje ani tam, kde by podle racionální analýzy měla (odpovědi 1A+2A). A naopak, lidé jsou ochotni podstupovat zcela iracionální riziko v případě, kde hrozí snesitelná ztráta (odpověď 3B).
Pokud si myslíte, že se jedná o zbytečné akademické rozjímání, pak se zkuste zamyslet ...
- kolik ubožáků nahází do "výherních" automatů vypůjčené peníze jen proto, že nedokážou správně posoudit své šance a ve falešném přesvědčení, že právě oni dokážou přelstít statistiku, padnou nakonec do ještě hlubší dluhové propasti.
- kolik lidí se rozhodne vyhnout lékařskému ošetření (operace, očkování atp.) a ohrožují sebe nebo ostatní, jen proto, že přeceňují rizika pohybující se těsně nad 0%.
- kolik lidí vynaloží zbytečné peníze za všemožné reklamní lákání a strašení (... šance, že se domůžete Vaší pohledávky je 95%, my Vám nabízím její odkoupení za 80% celkové ceny = 100% jistota, že přijdete o 15% majetku ... nebo, připlaťte si 20% za nové běžecké boty, které eliminují zranění o 5%, atp.)
- jak efektivně asi mohou fungovat složité finanční trhy, pokud lidé neumí vyhodnocovat racionálně zisk a ztrátu i v tak jednoduchých případech, jako jsem popsal výše (pro zajímavost: na popsané tři experimenty jsem se zeptal vybraných kamarádů, které považuji za nadprůměrně inteligentní, přičemž ani jedna odpověď nebyla v kombinaci 1B+2B+3A).
Váhy pravděpodobností
Skvělou knihou, která mě inspirovala k přemýšlení o statistických preferencích a o tom, jak lidé obvykle nedokážou správně vyhodnotit rizika, je Myšlení, rychlé a pomalé (Daniel Kahneman). Autor, nositel noblovy ceny z roku 2002, po dlouhodobém výzkumu sestavil dech-beroucí tabulku, která ukazuje, jaké váhy lidé přiřazují ve svých volbách jednotlivým pravděpodobnostem. Pravděpodobnost 1% obvykle nadhodnocují jako by se jednalo o 5,5% ... 99% jistotu naopak považují za pouhou 91,2% šanci atd.

A naděje, že se lidé změní? Patrně žádná není. Avšak každý, kdo si uvědomí, že jeho intuice není tak skvělým statistickým nástrojem, jak se domníval, ten má rozhodně možnost být příště ostražitějším a spoléhat více na logický úsudek ("pomalé myšlení"), spíše než na intuici ("rychlé myšlení").


